福岡県立修猷館高等学校同窓会 東京修猷会

『素粒子理論物理学ってなに？～素粒子が造り出す自然の美と数学的構造～』

講師：森山翔文さん(平成５年卒)
開催日時：令和3年7月8日(木) 19:00-20:00

○服部　執行部で二木会を担当しています昭和59年卒の服部です。今回も多数の皆さまにご参加いただき、ありがとうございます。
今回の二木会は、「素粒子理論物理学ってなに？～素粒子が造り出す自然の美と数学的構造～」というテーマで、平成５年卒業の森山翔文（もりやま さねふみ）さんにご講演いただきます。
　講演に先立ち、平成７年卒の寺口俊介さんに講師をご紹介いただきます。今日は講師と紹介者のお二人は関西からのご参加です。こちら東京の学士会館と合わせると、３カ所からの放映ということになります。

■講師紹介

〇寺口　私は森山さんの２年後輩でしたが、修猷では森山さんと面識はありませんでした。でも、森山さんが数学オリンピックの日本代表に選ばれた時のことはよく覚えています。全校生徒が講堂に集まって森山さんの壮行会を開きました。応援団のエールの後、森山さんは答辞で、「メダルが取れなかったら帰ってきません」とおっしゃり、私は「さすが修猷。すごい人がいる」と感心しました。後で話を聞いたところ、実は森山さんも内心では結構ひやひやされていたそうですが、見事に銅メダルを獲得され修猷に帰ってこられました。
　森山さんは東大に進学されましたが、私が３年生で受験する時、「森山は東大に行ったぞ」みたいなことを先生方からよく聞かされました。先生方としては、森山さんを見習って「おまえも頑張って東大を目指せ」という意味だったと思うのですが、私はむしろ森山さんに畏れをなして、東大に行くことはやめてしまいました。
　その後、京大の大学院の理論物理学の研究室で森山さんと再会しました。森山さんは東大に進学されていましたし、数学のイメージでしたので、おなじ研究室に所属することになるとは全然予想していなかったのですが、お名前と口調から、かの有名な数学オリンピックの森山さんだと気が付いて驚きました。森山さんは、学問一筋の厳しい人かと思っていたのですが、実際には大変お茶目な方で、研究室のハイキングや私が主催していたサークルの花見など楽しい思い出がいろいろあります。研究室では、森山さんと私は同じ師匠に付いた兄弟弟子になり、一緒に共同研究もさせていただきました。
　京大の大学院を卒業された後、森山さんはアメリカの名門Caltechに３年間留学されます。そして帰国後、名古屋大学に着任されます。
　一方、私は大学院を卒業後、台湾に留学しました。実は森山さんの母国は台湾で、10歳ぐらいの時に来日され、日本に帰化されています。私はそんな森山さんとゆかりのある台湾に留学し、帰国して帰った先が名古屋大学ということで、またもご縁があって森山さんと同じ所で研究することになりました。
　2008年に、南部さん、小林さん、益川さんの３名の日本人がノーベル物理学賞を取られたことを覚えていらっしゃる方も多いと思いますが、小林さんと益川さんは名古屋大学のＯＢです。受賞の時には、大学で森山さんと一緒にテレビ局からの取材を受けました。
　森山さんの生まれ故郷の台湾での研究会に一緒に参加したことがあります。森山さんはもちろん中国語が話せます。現地の秘書さんから、「中国語がうまいね」と褒められ、森山さんは「今は日本人だけれども、もとは台湾人」と答えましたら、「え、じゃ中国語は下手ね」と言われて森山さんはすっかりしょげていました。
　森山さんはその後、大阪市立大学に移られて、今年から教授に昇進されています。本日は森山さんの専門である超弦理論の最先端の研究の話を聞けるということで私も楽しみにしています。

■森山氏講演

〇森山　寺口さんに紹介を依頼した時、結婚式のスピーチをイメージすればいいですねと確認されて、少し不安でしたが、素敵な紹介ありがとうございます。また本日はこのような機会を与えてくださり、ありがとうございます。とても光栄です。

■はじめに

　今日は理論物理学のお話です。実は私は高校時代、物理があまり好きではありませんでした。例えば、高校の教科書には、電気回路として、コイルとコンデンサーを含むＬＣ回路の説明がグラフと共に書かれていますが、当時の私には、電流や電圧の増減の説明が複雑すぎて、その説明が正しいかどうか確信できませんでした。その後、微分方程式を勉強して初めて教科書の内容を理解することができました。その時に強く感じたのは、物理は微分方程式の概念なしでは語れない、微分方程式と一緒に理解すべきだということでした。
　微分方程式によって自然現象を理解するという研究手法は、ニュートンが初めて導入しました。それはペストの流行でケンブリッジ大学が休校になっていたときの話です。この事実は、コロナ禍の今、私たち理論物理学者の心の支えになっています。
　ニュートンによれば、運動方程式と万有引力を仮定すれば、リンゴの自由落下から惑星の楕円軌道運動まで、スケールを超えてすべて説明できることになります。これによって私たちの自然観が確立しました。その自然観を二点にまとめると、(1)物理量の時間発展は微分方程式により決まり、(2)宇宙の神羅万象は物理法則によって統一的に記述される、ということになります。その自然観は、本日の理論物理学に受け継がれています。
　今日の話を始める前に、まず注意しておきたいことがあります。今日は難しい話をすると思いますが、その内容の理解よりも、理論物理学の美しさを楽しんでいただきたいと思います。例えば、私たちがオペラを鑑賞するときには、難しいイタリア語を理解しているわけではありませんが、美しい世界に惹かれていきます。私たちにとって理論物理学とはオペラのようなものです。

■量子論と足し上げ

　物理量の時間発展は微分方程式から決まり、さらに宇宙の神羅万象はスケールを超えて物理法則によって統一的に記述されるというのが、私たちの自然観です。しかし、原子などのミクロの世界において、この自然観は修正されます。これまでの自然観を私たちは「古典論」と呼び、新しい自然観を「量子論」と呼びます。
　大学で量子論を勉強された方もいらっしゃると思います。特にシュレディンガーの波動方程式は有名で、皆さんもこれを中心に勉強されたかと思います。この波動方程式と、ハイゼンベルクが提唱した行列力学が、実は等価であるということが後にディラックによって示されました。現代的な視点からでは、ファインマンの経路積分により量子論が定式化されています。
　ここでは経路積分による量子論を、生物学の進化論との類似で説明します。そのために、まず、これまでお話しした微分方程式による古典論を少し書き換えておきます。生物学ではダーウィンによって進化論が提唱され、それをドーキンスが『利己的な遺伝子』という著書でさらに発展させました。同じように物理法則を私はここで「利己的な電子」と名付けておきたいと思います。「利己的な遺伝子」と比べると、「い」が抜けているだけです。生物学との類似で古典論を書き換えて、量子論の説明に繋げたいと思います。
　これまで初期条件から微分方程式によって時間発展を決める古典論を考えていましたが、代わりに、空間内に作用という量をばらまいて、電子がどのような運動をするかを議論する新しい古典論を考えたいと思います。物理学では一般に作用をアルファベットのSで表しますが、以下の議論ではお金を連想させて理解を助けるため、＄マークを用いて記します。そうすると、電子は作用（＝お金）が多い方に時間発展することが自然に想像できます。つまり、それまで微分方程式によって電子の運動を記述してきましたが、微分方程式の内容を再現するように、空間に作用という量をうまく定義して、それによって電子の運動を記述できるようにしたのが、古典論の書き換えになります。これはあたかも電子が利己的な意思を持っているように思えます。
　もちろん進化論で、「利己的な遺伝子」と言っても、決して遺伝子が利己的な意思を持って進化しているわけではありません。むしろ遺伝子は好き勝手に不規則に突然変異をして、その中から生存競争を通じて進化の方向が決められます。このような思想がまさに量子論の内容になります。つまり量子論では、ばらまいた作用という量によって様々な仮想的な時間発展が起き、そこから観測によって電子がどこにあるかが決まると考えます。具体的には、作用をたくさん獲得した電子もあれば、作用をあまり獲得できなかった電子もあります。作用をたくさん獲得した電子は、その後、観測確率が大きくなり、作用をあまり獲得できなかった電子は観測確率が小さくなります。

　言い換えると、量子論というのは、始状態と終状態を決めた上で、遷移する確率を計算する学問です。このとき、電子は仮想的に様々な経路を通って時間発展しますが、その経路をすべて作用の重みで足し上げるというのが経路積分の考え方です。さらには、相互作用を考えることもあります。相互作用は分岐によって表わされ、電子が生成と消滅を経る寄与も同様に足し上げます。
　この量子論が私たちの新しい自然観になります。古典論では微分方程式によって、初期条件からの時間発展を考えていましたが、量子論では始状態から終状態への遷移確率を計算することになります。その確率を計算する際に、途中の仮想的な経路をすべて足し上げます。
　ここで少し注意を述べておきます。作用に用いた＄マークは実数ではなく虚数です。ですので、お金をたくさん獲得した電子の観測確率が高いというより、電子が獲得した虚数の位相が同じなら強め合い、ずれていたら弱め合うというのが本当の説明です。説明のために＄マークを使っていただけです。
　経路積分による量子論の枠組みで、始状態と終状態を決めてその間の時間発展に関してすべての経路を足し上げるという説明をしましたが、量子論に限らず、足し上げという概念は自然科学に普遍的に存在しています。例えば数学では母関数を考えたり、統計力学では分配関数、生物学では進化論を考えたりします。さらに人文科学でも、経済学では「神の見えざる手」、政治学では民主主義の多数決など、現代において様々な学問や思想で、形を変えて足し上げの概念が登場しています。

■弦理論と足し上げ

　量子論の足し上げの概念に従って遷移確率を計算していくと、物理量に無限大が生じてしまいます。多くの研究者の努力によって、重力以外の相互作用、つまり電磁気力などの場合に、この無限大は問題にならず処理が可能になりました。しかし、重力の場合、この無限大が処理できないこともわかりました。そして、無限大が生じる主な原因は、相互作用点の特異性にあると考えられています。
　弦理論では、その特異性をうまく回避しています。弦理論において、途中に現れる様々な弦の状態についても足し上げます。この弦の振動モードは、重力を含む様々な相互作用粒子に対応しています。このとき、1次元の弦が時間発展をすると時空内に２次元面を描きます。相互作用点を面に膨らませると、どこで相互作用が起きたか特定されず、相互作用点の特異性が緩和されます。これが私たちが弦理論を考える主な理由です。この弦理論によって、矛盾のない重力の量子論を考えることができます。
　しかし、弦理論ではわからないことがたくさんあります。例えば、弦理論は９次元の空間で定義されていて、さらに非常に高い対称性を持っていることが知られています。ところが、実験的に観測できる素粒子標準模型は、私たちが住んでいる３次元空間上で、弦理論より小さな対称性に基づいて構成されています。ですから、弦理論から素粒子標準模型を導出することは、重要な研究テーマです。

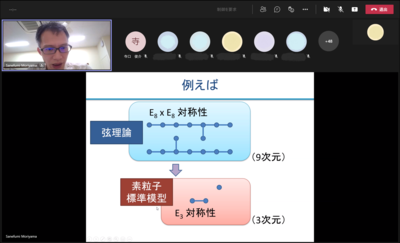
　さらに弦理論を詳しく調べますと、９次元理論だった弦理論が、特定の極限で10次元理論に拡大し、そこでは１次元の弦から２次元に広がった膜ができるということも知られています。この理論はＭ理論と名付けられ、ＭにはMembrane（膜の理論）、Mystery（謎の理論）、Miracle（奇跡的な理論）、Mother（母なる理論）など様々な期待が込められているそうです。弦理論の極限であるＭ理論を詳しく理解することは非常に重要です。

■私の研究

　最後に、弦理論やＭ理論における足し上げと関連して、Ｍ理論を特徴づけるある関数に関する私たちの研究を少しご紹介します。この関数は、高い対称性を用いて足し上げが実行され、その結果、数学的にも美しい多重積分になっています。私たちはこの関数を研究対象としています。

　この多重積分は有名なガウス積分の拡張です。物理的に、ガウス積分は、粒子の相互作用がないことを意味します。三体相互作用があれば指数が３次関数になりますが、ガウス積分の指数は２次関数ですので、相互作用がない、または、高い対称性によって相互作用の効果が相殺されていることを表しています。

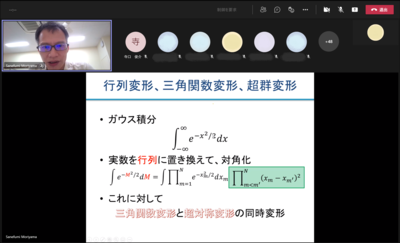
　このガウス積分にいくつかの変形を施せば、先ほどの多重積分に自然に到達します。ガウス積分というのは実軸上の積分ですが、その実数を行列に置き換えることをまず考えます。それに対して行列の対角化をすれば、図の緑色の関数が現れます。この関数に対して三角関数変形をすれば、正弦関数に似た黄色の双曲線関数に変わります。一方、緑色の関数に超対称変形を施せば、青色の関数に変わります。その両方の変形を同時に施した赤色の関数がＭ理論を特徴づける関数の中に被積分関数として入ってきます。

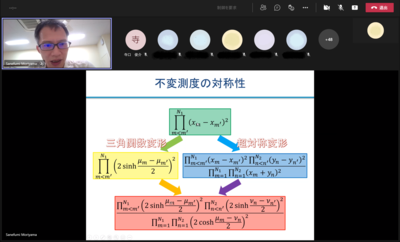
　素粒子論の最先端のＭ理論を特徴づける関数の計算から、この多重積分が得られましたが、仮に物理学を全く知らない数学者が、純粋に美しさだけを求めて拡張しても到達しうるくらい、非常に美しい多重積分になっています。究極的な物理理論において、このような究極的に美しい数式が出現します。私は約10年前にこの多重積分に出会って一目ぼれしました。そしてこんなに美しい多重積分がきれいに解けないわけがないと信じて研究に没頭し、その全容解明に励みました。
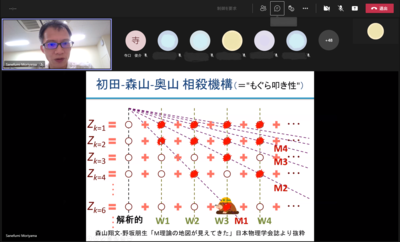
　その結果、解析的な部分が先にわかり、有名なエアリー関数になっています。また、それを超えた部分も、無限個の発散が相殺し、非常に調和が取れた形をしています。発散の相殺がもぐら叩きに似ていることから、私は「もぐら叩き性」と呼んでいますが、この性質は専門家から、私たちのイニシャルを付けて「ＨＭＯ（初田・森山・奥山）相殺機構」と呼ばれています。この美しい数学的な相殺機構は弦理論の特徴を捉えた非常に自然な性質です。

　これからこの分野で研究を始める若手研究者を対象に、これまでの私たちの研究成果を著書『Ⅿ理論と行列模型―超対称チャーン・サイモンズ理論が切り拓く数理物理学』にまとめましたので、興味があればご参照ください。この本の執筆を引き受けたときは、日本語だから簡単に書けると思っていましたが、実際に書いてみると説明がとても大変で、やっと昨年出版されました。このような進行中の研究成果を出版してくださったサイエンス社に感謝を申し上げます。

■振り返って

　物理学の目標は自然を理解することですが、そのために背後の数学的な構造を理解することを物理学と呼んでいいかどうか私にはわかりません。ニュートンの時代に数学と物理学の区別がありませんでしたから、最先端の科学では、その区別を気にする必要がないかもしれません。
　自分のこれまでを振り返ってみると、高校時代は数学少年だったと思います。高校時代に数学の斎藤先生と出会ったことは、間違いなく私の研究の根底にあります。それまで受験数学にしか興味がありませんでしたが、斎藤先生の導きにより、私はより広がりのある数学に接することができました。
　物理学に心から興味を持ったのは、おそらく大学の教養学部時代だと思います。東大の教養学部には、数学と物理学の垣根を超えた先生が多くいらっしゃいました。そこでは、抽象的に美しい数学は自然現象から抽出され、また物理学は美しい数学的な構造を兼ね備えて初めて大きく広がる、ということを学びました。
　大学院では京大に移り研究者を目指しましたが、理学部の研究職は非常に少なく、競争が激しいです。競争が激しすぎて研究が面白くなくなり、研究をやめようとした時期もありましたが、寺口さんのお話にも出てきた共同研究で自信を取り戻し、研究を続けることができました。その頃、修猷の同窓会に参加して、たぶん斎藤先生だったと記憶していますが、「研究職は少ないが、もしあれば採用されるか」と聞かれました。この言葉から、機会が巡ってきたときにそれを掴むだけの実力をつけておくことが大事だと諭していただいたように感じ、より一層研究に励むきっかけになりました。大変ありがたいことに、Caltechでのポスドク研究員を経て、名古屋大学で任期なしの助教として研究を行うことができるようになりました。私の研究の本質的な部分は、この時期に行われました。任期なしの助教職が非常に貴重なものであると実感しました。
　振り返れば、最初にお話しした物理への不満が私の研究の原動力だったかもしれません。ＬＣ回路の説明に対する不満でより緻密な微分方程式が必要だったのと同じように、今の弦理論の発展でもより緻密な数学が必要で、そのような数学を開発していくのが私の研究テーマであり、ライフワークだと考えています。
　最後に若手へのメッセージを述べさせていただきたいと思います。私たちは資本主義の中に生きていますので競争は否定できませんが、初心を忘れずに、様々な出会いを通じて、自分のやりたいことを見つけてほしいと思います。私たちもしっかりお手伝いをしていきたいと思います。

■会長あいさつ

〇伊藤　今日のお話にありましたように、外国語のオペラは何を言っているのかは分かりませんが、その美しい調べを心から楽しみます。今日の弦理論のお話は、まるでオペラを聴いているような気分でした。
　森山さんは、高校時代の先生との出会いの中で数学というものに、そして大学に入られて物理というものに興味を持ち始めて、そして現在の研究生活があるということでした。私たちの東京修猷会は、修猷館を母校とする人たちが集まっているわけですが、やはり高校時代の、先生との出会いも含めてのいろいろな出会いやきっかけが、その後の人生に大変大きな意味合いを持っているのだと思います。またそのような高校時代のよき思い出が、同窓というだけで心がつながる一つの大きな要因なのだろうと思います。
　今日は、大変優秀な数学者であり、そして物理学者としての森山さんの研究の一端を垣間見たのですが、修猷館の同窓生がこのように先端的な分野で大活躍されていて、大変心強く思いました。
　今はコロナで、いろいろな交流が難しくなっていますが、このようなオンラインでの講演会で、同窓の人たちが頑張っている姿を見ることができて大変よかったと思います。これからもこのような会合を続けていきたいと思っています。

（終了）